찌몸통 모양에 따른 기능 분석

[출처] 입큰붕어 : 찌연구소>2176 윤석아빠님

그림4

찌몸통 모양에 따른 기능 분석

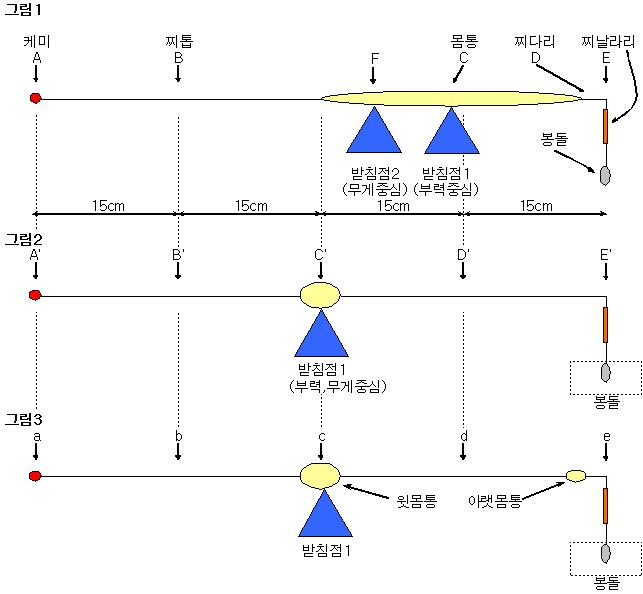
찌의 5가지 기본구성 요소인 케미, 찌톱, 몸통, 찌다리, 찌날라리의 무게가 각각 1g인
가상의 찌 2개가 있습니다.


찌의 총무게는 똑같이 5g이지만 몸통의 모양은 위 그림1,2와 같습니다.
오뚜기 찌의 무게중심과 부력중심은 모두 몸통 중앙에 존재 하고 있겠지요!
하지만 막대찌의 무게중심과 부력중심은 서로 다른 위치에 있습니다.
각 구성요소의 개별적인 무게중심의 위치(A~E, A'~E'))는 그림과 같습니다.

막대찌를 손가락위에 올려 확인한 무게중심 위치는 받침점2 F지점 입니다.
(위 그림을 손가락위에 올려놓을 수 없기에 회전토오크 구하는 방식으로
계산하여 구해진 위치로, 힘점 E로부터 24.4cm에 위치합니다.)

찌를 일으켜 세우기 위해서는 봉돌이 아래로 잡아당기는 힘이 필요하고
찌를 떠받히는 받침점1(부력중심)이 필요합니다.

따라서 막대찌가 기립하기 위해서는
최소한 받침점1을 기준으로 하는 좌우의 평형이 이루어져야 하므로
평형에 필요한 2.625g의 봉돌무게가 소요됩니다.

이때 받침점1에 가해지는 무게는
찌무게5g + 봉돌무게2.625g = 7.625g 이고,
그림2의 오뚜기찌는 찌무게5g + 봉돌무게0.000g = 5.000g 입니다.
같은 길이, 같은 무게의 찌임에도 받침점에 가해지는 무게에 차이가 발생합니다.

그래서 길이가 같고, 기립의 성능을 똑같이 하기 위해서는
막대찌의 몸통을 오뚜기찌의 몸통보다 크게 만들어야 합니다.

만일 막대찌와 오뚜기찌의 몸통을 같은 크기(부피)로 만들었다면
“막대찌가 기립을 하지 못하고 입수할 가능성이 크다” 라고 할 수 있고,
몸통의 크기가 막대찌가 기립을 무난히 할 수 있다면
같은 몸통 크기의 오뚜기찌는 찌톱을 더 길게 설계할 수 있습니다.


위 그림1의 막대찌에 대한 예를 들어보겠습니다.
첫 번째 : 위 그림1의 막대찌에서 케미의 무게를 1g 증가시키면 다시 평형을 이루기 위해서는 2.75g의 봉돌이 필요합니다.
증가한 케미의 무게 1g + 늘어난 봉돌무게 2.75g = 3.75g
즉 케미는 자신의 무게의 3.75배로 받침점1에 영향을 미칩니다.

두 번째 : 찌톱의 무게를 1g 증가시키면 다시 평형을 이루기 위해서는 1.8125g의 봉돌이 필요합니다.
증가한 찌톱의 무게 1g + 늘어난 봉돌무게 1.8125g = 2.8125g
즉 찌톱은 자신의 무게의 2.8125배로 받침점1에 영향을 미칩니다.

세 번째 : 몸통의 무게를 1g 증가시키면 시이소 평형에 지장을 주지 않기에
봉돌의 가감이 필요 없습니다.
증가한 몸통의 무게 1g + 늘어난 봉돌무게 0g = 1.0g
즉 몸통은 자신의 무게의 1.0배로 받침점에 영향을 미칩니다.

네 번째 : 찌다리의 무게를 1g 증가시키면 다시 평형을 이루기 위해서는
0.9375g의 봉돌을 감소시켜야 합니다.
증가한 찌다리의 무게 1g + 늘어난 봉돌무게 (-0.9375g) = 0.0625g
즉 찌다리는 자신의 무게의 0.0625배로 받침점에 영향을 미칩니다.

다섯 번째 : 찌날라리의 무게를 1g 증가시키면 다시 평형을 이루기 위해서는
1g의 봉돌을 감소시켜야 합니다.
증가한 찌다리의 무게 1g + 늘어난 봉돌무게 (-1.0g) = 0.0g
즉 찌날라리는 자신의 무게는 봉돌의 크기만 줄여줄 뿐 받침점에는 전혀 영향을 미치지 아니합니다.

“찌의 각각의 구성요소가 받침점에 미치는 영향력이 서로 다르지만
오뚜기찌와 막대찌가 또 다른 결과가 나오네요?”
네 그렇습니다.
그 이유는 각각의 구성요소의 위치가 변하였기 때문입니다.

위 그림1과 같이 몸통의 모양과 찌다리의 길이가 다른 상태에서
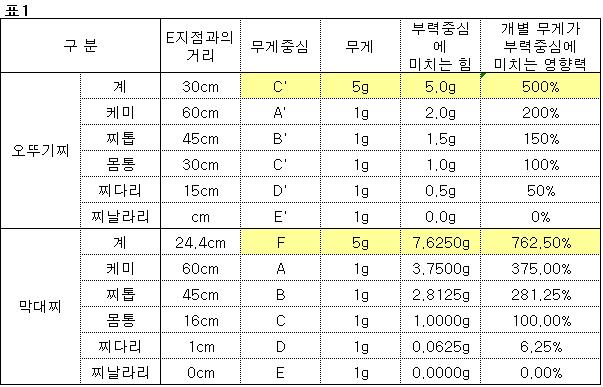
각각의 구성요소에 대한 특징은 표1과 같습니다.
표1 참조


표1 에서 보시다시피 케미의 무게가 기립입수에 가장 큰 악영향을 미치고 있지만
막대찌의 케미가 오뚜기찌의 케미보다 더 큰 악영향을 끼치고 있음을 알 수 있습니다.

기립입수에 지장을 초래하는 순서는 똑같이 케미>찌톱>몸통>찌다리 순이지만
그 영향력의 크기는 막대찌와 오뚜기찌가 서로 같지 않습니다.
또한 날라리를 제외한 찌의 모든 요소(부품)의 무게는 기립입수에 지장을 초래합니다.
===============================================================


이제는 몸통이 위, 아래 두 개인 찌 이야기를 하겠습니다.

흔히 “이중부력(二重浮力)찌” 라고 용어를 붙여 사용하고 있으나
힘(力)은 크기, 방향, 위치로만 표현합니다.
힘에 모양이 있을 수 없고, 모양을 힘으로 나타낼 수 없기에
저는 편의상 “분할몸통” 이란 용어로 사용함을 양해하여 주시길 바라며
혼돈하지 말 것을 부탁드립니다.

그림3은 그림2와 동일한 조건에서 E지점으로부터 3cm거리에
무게 0.1g, 부피 1㎤의 아랫몸통을 부착하였습니다.
이로 인하여 받침점이 약간 오른쪽으로 이동하였고,
부력중심과 무게중심이 일치하지 않는 상태가 되었습니다.

이 아랫몸통은 중력(0.1g)과 부력(1g)모두 작용하고 있으나
중력보다는 부력이 크기 때문에 기립입수에 도움이 됩니다.
하지만 위치가 E지점으로 부터 너무 가까이 붙어있어 그 영향력은 미약할 것입니다.

각각의 몸통을 회전토오크 방식으로 나타내 본다면 아래와 같습니다.

윗몸통 부피를 10㎤ 이라고 가정하겠습니다.
윗몸통 : 부피 10㎤ × E지점으로 부터 거리30cm = 300g/cm
아랫몸통 : 부피 1㎤ × E지점으로 부터 거리3cm = 3g/cm

찌를 기립입수 하는데 있어 윗몸통은 300g/cm의 힘으로 작용하는데 반하여
아랫몸통은 3g/cm의 힘으로 작용하고 있음을 알 수 있습니다.
따라서 아랫몸통은 찌를 기립입수 하는데
윗몸통의 1/100의 밖에 영향을 미치지 아니 하는 것입니다.

그림1의 막대찌를 “갑”이라 하고,
그림2의 단일몸통일 경우를 “을”이라 하며,
그림3의 분할몸통일 경우를 “병”이라 하겠습니다.
또한 분할된 두 개의 몸통을 합산한 부피(11㎤)와
같은 크기의 단일몸통일 경우를 “정”이라 하겠습니다.

“갑”의 몸통에 의한 회전토오크 = 160g/cm
“을”의 몸통에 의한 회전토오크 = 300g/cm
“병”의 몸통에 의한 회전토오크 = 303g/cm
“정”의 몸통에 의한 회전토오크 = 330g/cm

결론 : “아랫몸통은 찌를 일으켜 세우는데 별 도움이 안 된다”
==========================================================


“원줄의 사선입수” 문제는 계산으로 확인하는데
솔직히 제 능력에 한계를 느끼는 부분입니다.

원줄의 사선입수는 찌맞춤의 차이에 의하여 발생하기도 하지만
찌의 입수시간도 사선입수에 영향을 미친다고 생각합니다.

찌의 입수시간을 최대한 지연시킨다면
봉돌을 찌가 서있는 위치의 수직하방에 근접시킬 수 있습니다.

그림3의 분할몸통은 아랫몸통에서도 유체저항이 발생하므로
입수지연 효과는 “병”>“정”>“을”>“갑”일 것이고,
“갑”과 “을”의 차이는 크지만
“병”과 “정”의 차이는 별로 크지는 않을 것으로 추정합니다.
===========================================================


이번에는 스텔라님의 질문과는 관계가 없지만
원줄의 사선입수라는 관점에서 저의 생각을 이야기 하고자 합니다.

상당수의 조사님들은 유동채비가 원줄의 사선입수를 줄여준다고 합니다.
저도 한때는 유동채비가 원줄의 사선입수를 줄여준다고 생각했었습니다.
그런데 최근에 와서는 자꾸 의문점이 생기곤 합니다.

유동채비가 입수시간을 지연시키는 것은 사실이지만
찌고무가 아랫멈춤고무에서 윗찌멈춤고무까지(유동간격) 이동하면서
입수를 지연하는 인터벌은 봉돌을 찌 수직하방으로 당겨오는데
별 도움이 되지 않을 거라 생각합니다.
그래서 “유동채비에 의한 입수지연효과가 원줄의 사선입수를 줄여줄 수 있을까” 라는
의문이 자꾸 들면서도 이를 계산으로 풀어보기에는
저의 능력에 한계를 느끼기에 고민으로만 남아 있습니다.

물속에서의 무게가 5g이 되는 봉돌이 있습니다.
투척 후 봉돌은 수직으로 가라앉습니다.(봉돌이 밑으로 내려가려는 종력)
그런데 원줄이라는 방해요소로 인하여 봉돌이 수직으로 내려가는 힘이 점점 줄어듭니다.
밑줄이 수직으로 서게 되면 봉돌은 더 이상 내려갈 수가 없습니다.
밑줄이 잡아당기기 때문입니다.

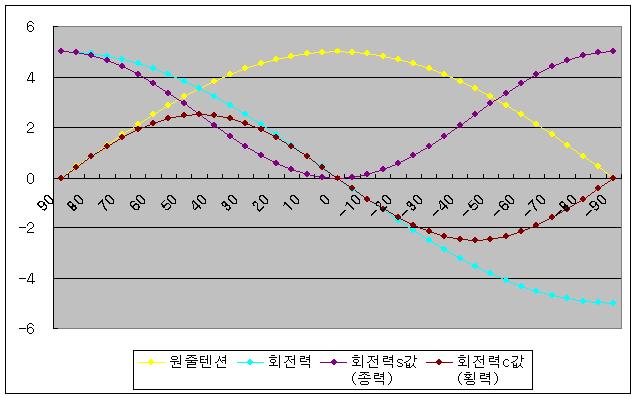
밑줄(찌고무와 봉돌 사이의 원줄)과 수직선간의 각도에 의해서 봉돌이 당겨오게 됩니다.(봉돌이 찌 하방 수직선 쪽으로 당겨져 오는 횡력. 45°에서 가장 큰 힘이 발생됨)
밑줄이 수직으로 서게 되면 봉돌은 찌 하방 수직선 쪽으로
더 이상 당겨올 수가 없습니다.
또한 봉돌을 당겨오는 힘의 반작용에 의해 윗줄(찌고무와 초릿대 사이의 원줄)이
일직선으로 펴지는 효과가 있습니다.

위 두 힘의 벡터합력으로 인하여 봉돌이 부채꼴을 그리며
찌고무를 중심으로 하는 회전력이 발생합니다.
이 회전력 역시 밑줄이 수직으로 서게 되면 없어지게 됩니다.

투척 후 밑줄에 발생하는 인장력(텐션)은 0에서
밑줄의 각도에 따라 커지다가 밑줄이 수직으로 서게 되면 최대가 되며,
봉돌의 물속무게와 같아집니다.

위와 같은 밑줄의 각도에 따라 변화하는 네가지의 힘은 그림 4와 같습니다.
참고로 알아두시기 바랍니다.


봉돌을 당겨오는 힘(횡력)의 반작용에 의해 윗줄이
일직선으로 펴지는 효과가 있습니다.

유동채비에서 유동의 간격을 넓히면 윗줄이 더욱더 잘 펴집니다.
이러한 이유로 봉돌을 최대한 멀리 안착될 수 있는 한계까지
보낼 수 있는 것입니다.
이에 대한 장점은 밑밥을 한곳에 모아놓는 것입니다.

봉돌을 최대한 멀리(maximum) 안착시키는 것이
원줄의 사선입수를 줄일 수 있을까요?

이러한 이유로 내림낚시에서는 원줄의 사선입수를 줄이기 위해
유동채비를 하면서도 유동간격을 두지 않는 이유라고 생각합니다.

제가 알고 있는 원줄의 사선입수를 예방하는 방법입니다.
1. 투척 후 낚싯대를 당겨놓았다가 다시 밀어놓는 방법
2. 투척 후 낚싯대 손잡이를 들어 올려 초릿대를 처박고
윗줄이 가라앉고, 찌톱이 입수를 시작하면 손잡이를 다시 받침대 거치하는 방법
3. 유체저항이 큰 찌(오뚜기찌)를 사용하여 입수시간을 지연하는 방법
4. 고부력찌를 사용하는 방법
5. 유동채비의 유동 폭을 두지 않는 방법
6. 찌맞춤을 가볍게 하고, 미끼를 작게 다는 방법

사선입수의 각도가 심각하지만 않다면 찌올림에서의 손해는 생각처럼 크지 않습니다.
붕어가 봉돌을 물고 어느 각도로 이동하느냐에 따라 다르지만
봉돌이 수직으로 상승한다는 전제하에서는
원줄의 사선입수가 찌올림에 미치는 영향은 미미합니다.

분할 몸통으로 사선입수를 약간은 줄일 수 있지만
찌의 기립에도 별 도움이 안 되고,
원줄과 엉켜서 찌가 더 가라앉는 불편만을 초래합니다.
그래서 분할몸통을 찌의 기능적인 측면에서는 사족(蛇足)이라고 생각합니다.

모양이나 멋을 내기 위한 방편이라면 괜찮습니다.